- ホーム
- >実 験
- >AIによる時系列データの未来予測
|
Pythonを使用た
回帰ニューラルネットワークRNNで 時系列データの未来予測 |
|
AIのRNN回帰ニューラルネットワークに、一定時間間隔毎にサンプルした既存の時系列データを入力し
未来どのような値になるかを予測することを試みます。
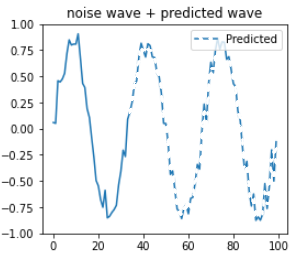
入力する時系列データは、教師データが明確な Sin波(Y=sin(Θ))に平均0、標準偏差1の正規分布の乱数を0.1倍したノイズを加算した波形を使用します。 下図の実線が既存の時系列入力データ、破線が未来の予測データ、教師データです。 |
 |
|
RNN回帰ニューラルネットワークの構成です。
|
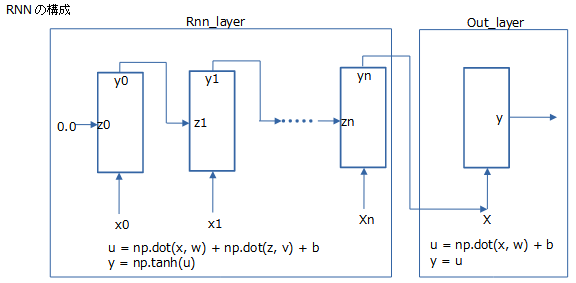
時系列入力データxの重みパラメータw、前時刻のRNN出力Yを入力したZの重みパラメータV
bはバイアス値で初期値0です。 |
|
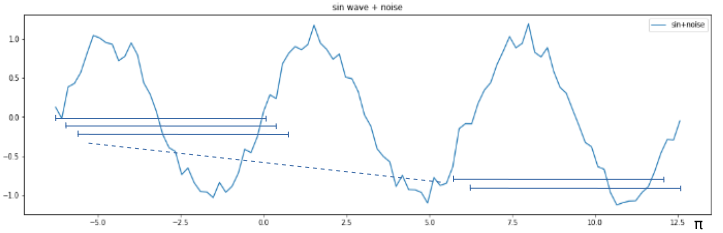
まず、振幅±1.0、長さ6πのsin波に、平均0、標準偏差1の正規分布の乱数を0.1倍したノイズを加算して
noise+sin波形(ノイズsin波形)を作成します。
作成した6πのノイズsin波形を時間軸方向に100分割して、指定個数の連続したサンプル値を1個づつずらしながら配列へ保存します。 その配列のデータをRNNへ入力して学習します。 指定個数の連続したサンプル値をRNNへ入力し演算した結果は、指定個数+1個目のサンプルデータの予測値として、 ノイズsin波の実際の値との二乗和誤差を計算します。この誤差が小さくなるようにRNNの重みパラメータを更新します。
二乗和誤差 = Σk(yk-tk)2/2
|
 |
|
6πのノイズsin波を全て学習することを1Epochとして100Epoch学習してみました。
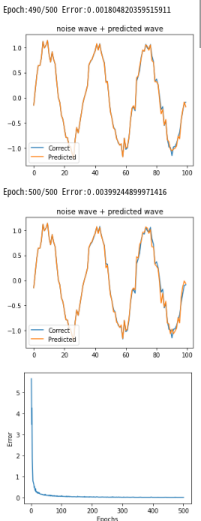
予測方法 学習完了後、RNNにノイズsin波形のスタート時のデータ10個を与え、ノイズsin波10データから 次の11番目の波形を予測します。 予測値をノイズsin波の配列の最後に加え、又、配列の最初のデータを捨て、合計10個のデータを RNNに与え次の12番目の波形を予測します。 これを繰り返してスタート時の10個目以降の波形を順次予測します。 下記グラフはEpochが進むにつれてRNNが学習し、青色のノイズsin波に対しオレンジの予測波形が 重なっていく様子を表示しています。 RNN個数:10、中間層:20、学習係数:0.0005、Epoch:100 |
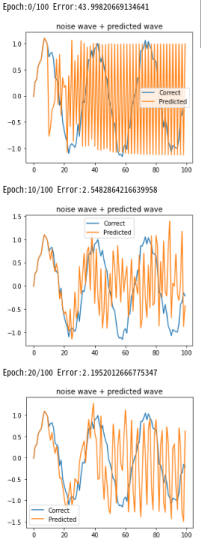
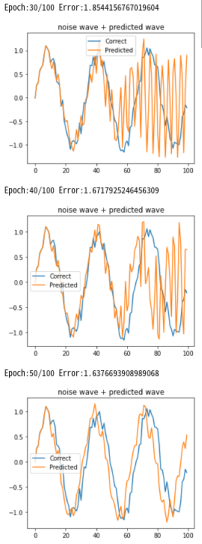
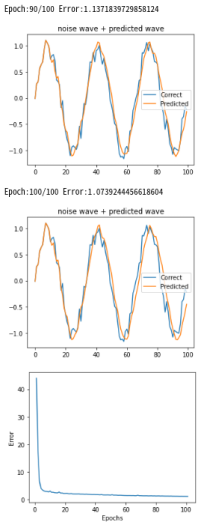
青色:ノイズsin波
オレンジ:予測波形、 青とオレンジが重なった部分:開始時のみRNNへ10個のノイズsin波データを入力 |
重みの初期値にxavierの初期値を使用するとRNN個数、中間層個数、学習回数を増やすことで
Errorが改善しました。
Errorが改善しました。
|
1回目
Epoch:0/50 Error:10.997 Epoch:10/50 Error:1.144 Epoch:20/50 Error:0.905 Epoch:30/50 Error:0.865 Epoch:40/50 Error:0.834 Epoch:50/50 Error:0.807 |
2回目
Epoch:0/50 Error:12.052 Epoch:10/50 Error:0.988 Epoch:20/50 Error:0.787 Epoch:30/50 Error:0.702 Epoch:40/50 Error:0.650 Epoch:50/50 Error:0.605 |
|
1回目
Epoch:0/50 Error:6.011 Epoch:10/50 Error:0.305 Epoch:20/50 Error:0.291 Epoch:30/50 Error:0.278 Epoch:40/50 Error:0.280 Epoch:50/50 Error:0.272 |
2回目
Epoch:0/50 Error:5.463 Epoch:10/50 Error:0.331 Epoch:20/50 Error:0.310 Epoch:30/50 Error:0.299 Epoch:40/50 Error:0.300 Epoch:50/50 Error:0.292 |
|
1回目
Epoch:0/50 Error:4.619 Epoch:10/50 Error:0.743 Epoch:20/50 Error:0.405 Epoch:30/50 Error:0.386 Epoch:40/50 Error:0.297 Epoch:50/50 Error:0.285 Epoch:60/100 Error:0.266 Epoch:70/100 Error:0.239 Epoch:80/100 Error:0.241 Epoch:90/100 Error:0.207 Epoch:100/100 Error:0.185 |
2回目
Epoch:0/50 Error:5.270 Epoch:10/50 Error:0.956 Epoch:20/50 Error:0.461 Epoch:30/50 Error:0.361 Epoch:40/50 Error:0.313 Epoch:50/50 Error:0.279 Epoch:60/100 Error:0.280 Epoch:70/100 Error:0.223 Epoch:80/100 Error:0.212 Epoch:90/100 Error:0.187 Epoch:100/100 Error:0.196 |
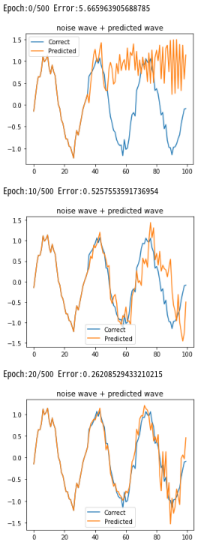
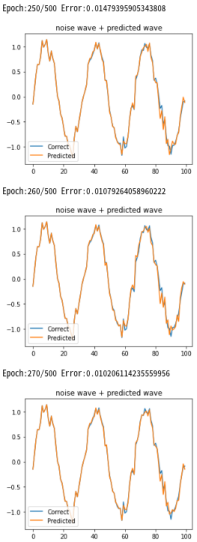
|
|
|
|
実運用を考えた時、ノイズは常に変化し、波形の振幅、位相も、運用時の条件によって変化します。
同一波形を予測するのではなく、ノイズが変化した、振幅を変えた、位相を変えた波形をRNNへ入力し、
0.6周期分の入力波形から2周期〜3周期の波形を予測できるかを検証します。
1回目 検証として、学習時と異なるノイズ波形、振幅を変えたノイズsin波を RNNへ0.6周期分入力し 2周期〜3周期の波形の平均値、sin波を予測します。 ランダムノイズ波形を含めて予測することは無意味と思われるので、その平均値を予測します。 波形が重なった部分が1周期分のサンプル値で、それ以降が赤色:予測波形となります。 フィルターではありませんので3周期分の時系列データをRNNへ入力して sin波を出力しているわけではありません。 RNN個数:20、全波形分割数:100 左図:振幅1.0のノイズsin波形 中央:振幅0.5のノイズsin波形 右図:振幅0.5の理論値sin波形 |
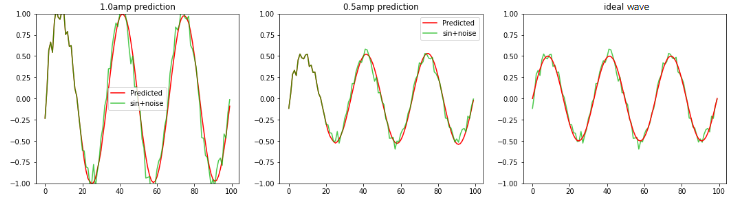
緑色:ノイズsin波
赤色:予測波形、 緑と赤色が重なった部分:開始時のみRNNへノイズsin波データを入力 振幅1.0のsin波を予測出来ました、また振幅を0.5へ変えましたが、理論値に近い値で予測出来ました。 |
|
学習時と異なる位相、ノイズ波形、振幅を変えたノイズsin波を
RNNへ0.6周期分入力し
2周期〜3周期の波形の平均値、sin波を予測します。
左図:振幅1.0のノイズsin波形 中央:振幅0.5のノイズsin波形 右図:振幅0.5の理論値sin波形 |
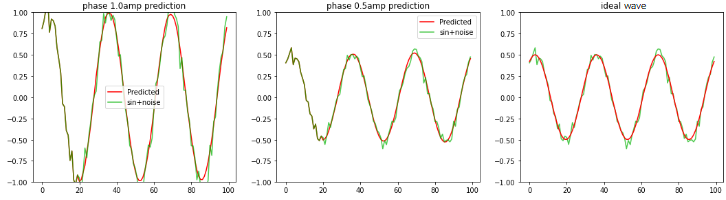
位相と振幅を変えましたが、理論値に近い値で予測出来ました。
|
|
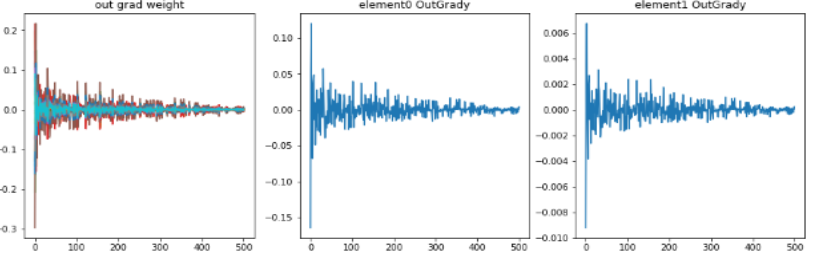
学習時のoutLayerの重みが少し変化したとき誤差の微分値、勾配の推移。
|
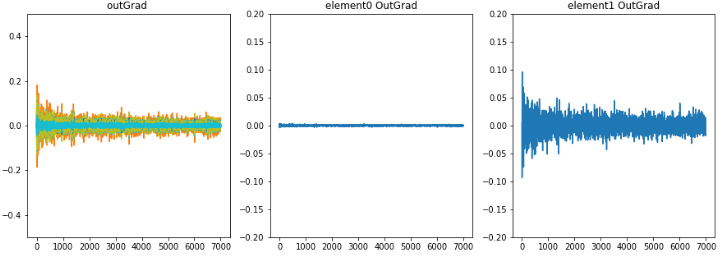 |
|
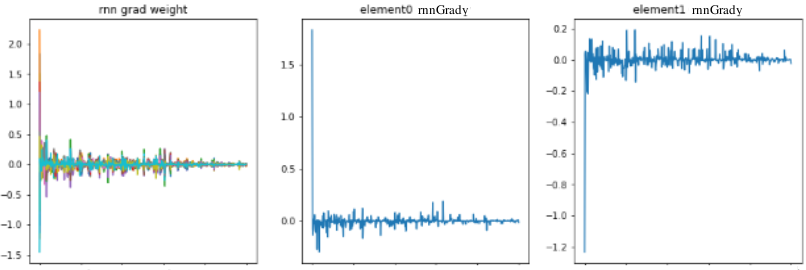
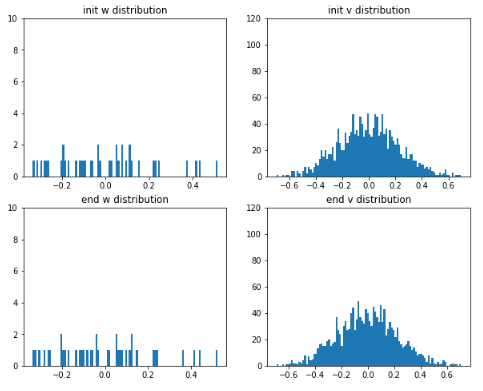
学習時のRnnLayerの重み分布とerrorの推移
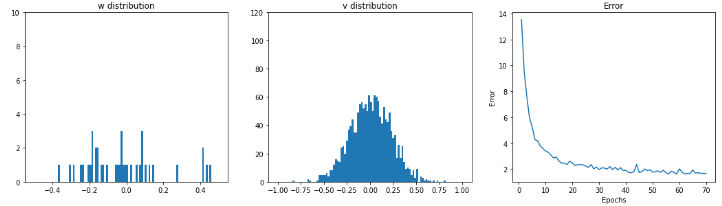 |
|
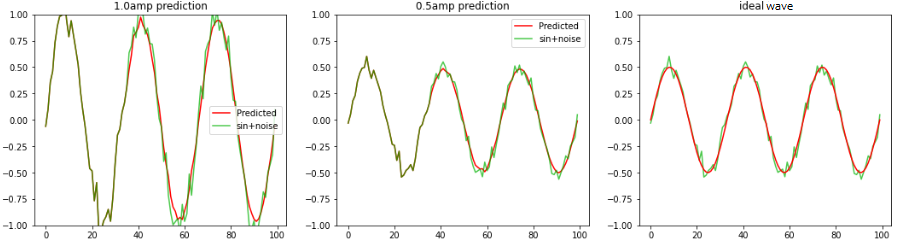
2回目
学習時と異なるノイズ波形、振幅を変えたノイズsin波をRNNへ 1.1周期分入力し2周期〜3周期の波形の平均値、sin波を予測します。 LSTM個数:36、全波形分割数:100 左図:振幅1.0のノイズsin波形 中央:振幅0.5のノイズsin波形 右図:振幅0.5の理論値sin波形 |
 |
|
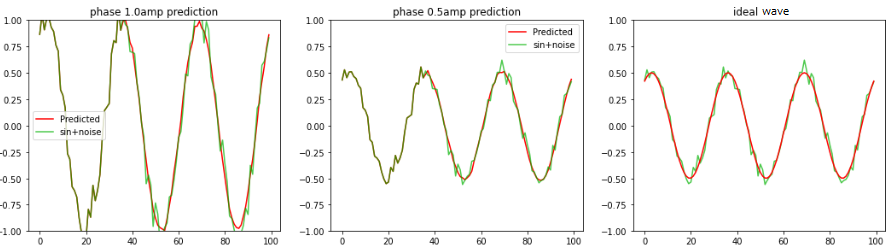
学習時と異なる位相、ノイズ波形、振幅を変えたノイズsin波をRNNへ
1.1周期分入力し、2周期〜3周期の波形の平均値、sin波を予測します。
左図:振幅1.0のノイズsin波形 中央:振幅0.5のノイズsin波形 右図:振幅0.5の理論値sin波形 |
 |
|
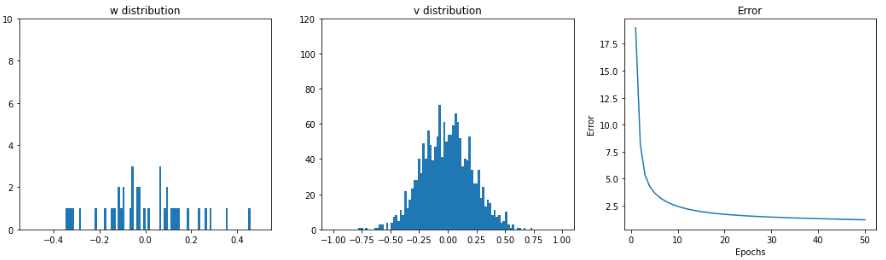
学習時のRnnLayerの重み分布とerrorの推移
 |
|
以上の結果からRNNを使用してノイズ波形、波形の振幅、位相を変更しても、与えた1周期分の時系列データから
2〜3周期の波形を十分に予測することが出来ました。
|
|
今回はLSTM(Long short term memory長期短期記憶)を使用します。
前回同様、同一波形を予測するのではなく、ノイズが変化した、振幅を変えた、位相を変えた波形をLSTMへ入力し、
0.6周期分の入力波形から2周期〜3周期の波形を予測できるかを検証します。
学習時間は3倍程度遅くなりますが、予測精度が高くなりました。
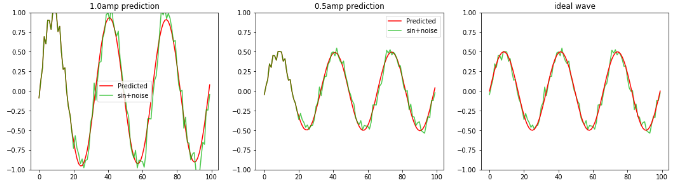
検証として、学習時と異なるノイズ波形、振幅を変えたノイズsin波を LSTMへ0.6周期分入力し 2周期〜3周期の波形の平均値、sin波を予測します。 波形が重なった部分が0.6周期分のサンプル値で、それ以降が赤色:予測波形となります。 LSTM個数:20、全波形分割数:100 左図:振幅1.0のノイズsin波形 中央:振幅0.5のノイズsin波形 右図:振幅0.5の理論値sin波形 |
 |
|
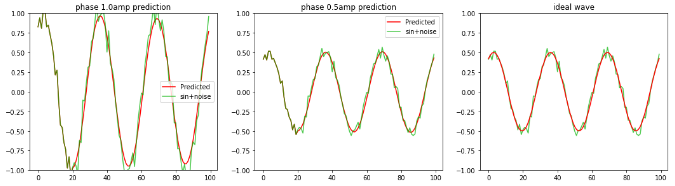
学習時と異なる位相、ノイズ波形、振幅を変えたノイズsin波を
LSTMへ0.6周期分入力し
2周期〜3周期の波形の平均値、sin波を予測します。
左図:振幅1.0のノイズsin波形 中央:振幅0.5のノイズsin波形 右図:振幅0.5の理論値sin波形 |
 |
|
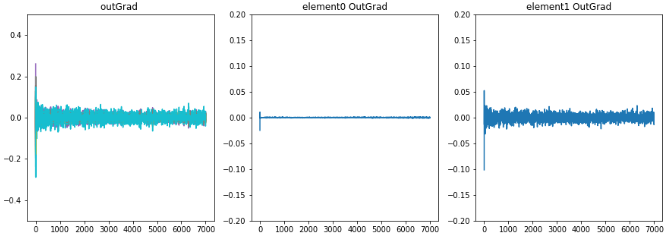
学習時のoutLayerの重みが少し変化したとき誤差の微分値、勾配の推移。
|
 |
|
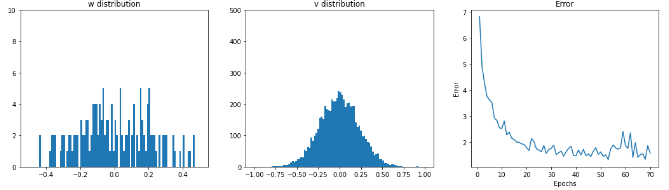
学習時のLSTMLayerの重み分布とerrorの推移
 |
|
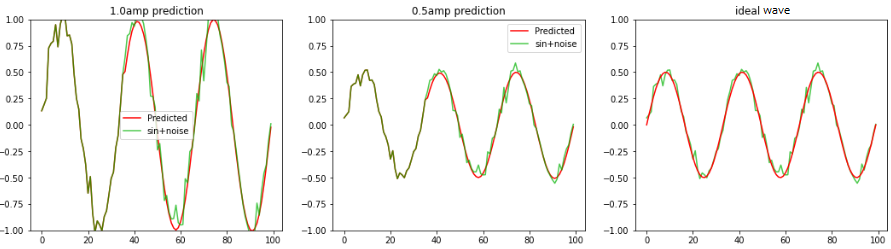
2回目
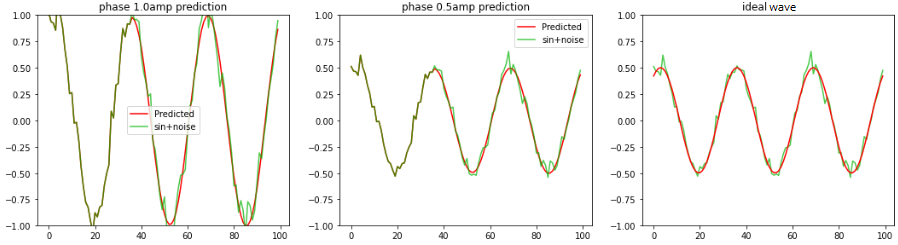
学習時と異なるノイズ波形、振幅を変えたノイズsin波を LSTMへ1.1周期分入力し 2周期〜3周期の波形の平均値、sin波を予測します。 波形が重なった部分が1.1周期分のサンプル値で、それ以降が赤色:予測波形となります。 LSTM個数:36、全波形分割数:100 左図:振幅1.0のノイズsin波形 中央:振幅0.5のノイズsin波形 右図:振幅0.5の理論値sin波形 |
 |
|
学習時と異なる位相、ノイズ波形、振幅を変えたノイズsin波を
LSTMへ1.1周期分入力し
2周期〜3周期の波形の平均値、sin波を予測します。
左図:振幅1.0のノイズsin波形 中央:振幅0.5のノイズsin波形 右図:振幅0.5の理論値sin波形 |
 |
|
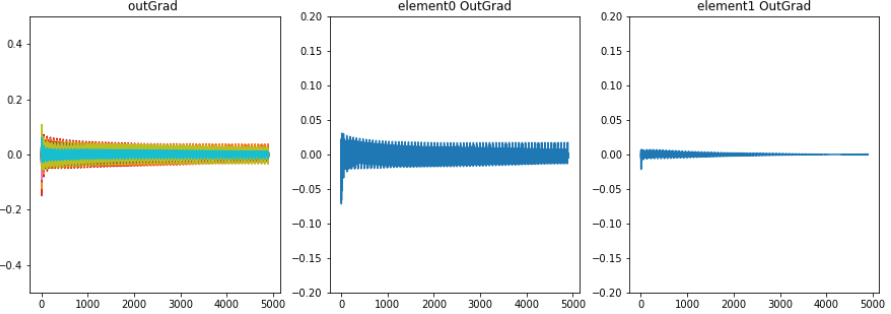
学習時のoutLayerの重みが少し変化したとき誤差の微分値、勾配の推移。
|
 |
|
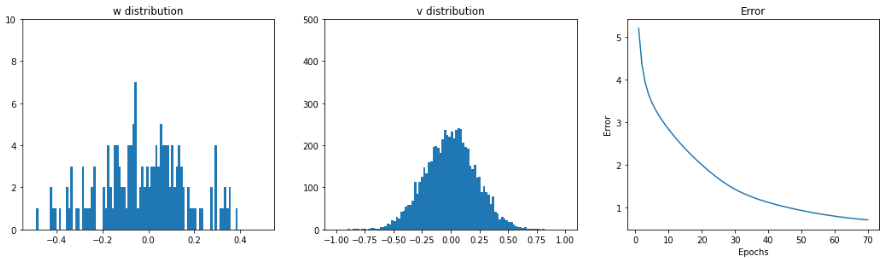
学習時のLSTMLayerの重み分布とerrorの推移
 |
|
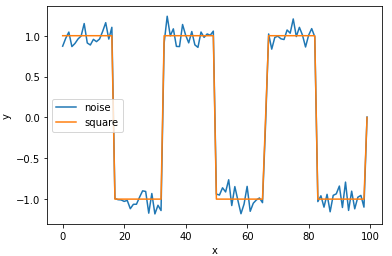
LSTMニューラルネットワークに、ノイズを重畳した矩形波の時系列データを入力し 未来どのような値になるかを予測することを試みます。
青色がノイズを重畳した矩形波、オレンジ色が未来の予測波形,教師データです。波形が重なっているので見えませんが
青色はノイズを重畳した矩形波です。
|
 |
|
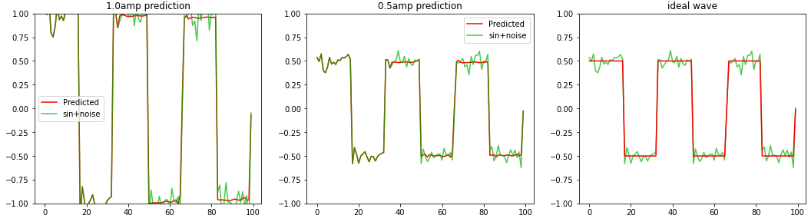
下図、学習時と異なるノイズ波形、振幅を変えたノイズ矩形波を
LSTMへ1.1周期分入力し
2周期〜3周期の平均波形、矩形波を予測します。
波形が重なった部分が1.1周期分のサンプル値で、それ以降が赤色:予測波形となります。 左図:振幅1.0のノイズ矩形波 中央:振幅0.5のノイズ矩形波 右図:振幅0.5の理論値矩形波 |
 |
|
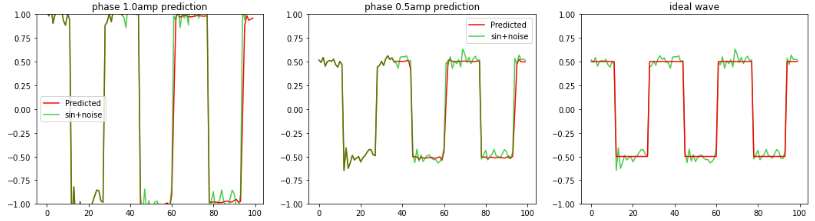
学習時と異なる位相、ノイズ波形、振幅を変えたノイズ矩形波を
LSTMへ1.1周期分入力し
2周期〜3周期の平均波形、sin波を予測します。
左図:振幅1.0のノイズ矩形波 中央:振幅0.5のノイズ矩形波 右図:振幅0.5の理論値矩形波 |
 |
|
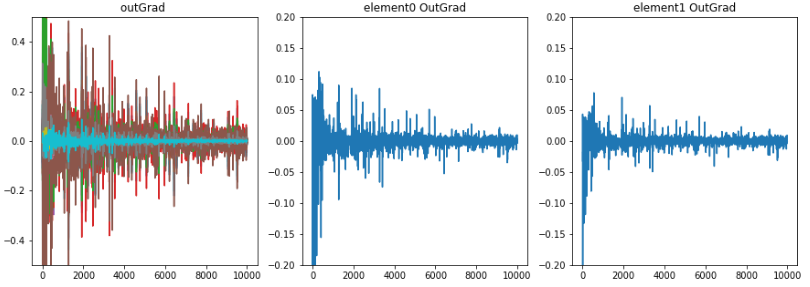
学習時のoutLayerの重みが少し変化したとき誤差の微分値、勾配の推移。
|
 |
|
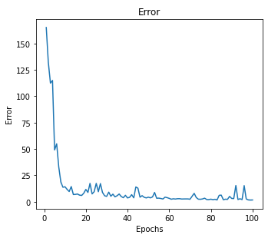
学習時のLSTMLayerのerrorの推移
 |