- ホーム
- >実 験
- >AIによる複数時系列データの予測
|
Pythonを使用た
回帰ニューラルネットワークRNNで 時系列データの未来予測2 |
|
前項では単一入力のRNN回帰ニューラルネットワーク,LSTM(Long short term memory長期短期記憶)
を使用して時系列データの未来予測を行いました。
今回、複数入力のRNN,LSTMを使用した時系列データの予測を行います。
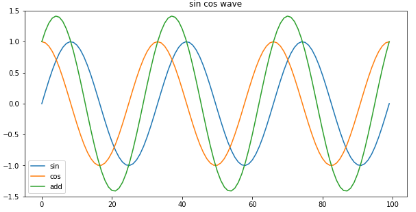
一定時間間隔毎にサンプルした既存の2種の時系列データを入力し どのような出力値になるかを予測することを試みます。 入力する時系列データは、教師データが明確な sin波、cos波を使用し、sin+cosの合成波を予測します。 |
 |
|
RNN,LSTMへ一定時間間隔毎にサンプルした時系列データ、ノイズsin波、ノイズcos波を入力し、 教師データとしてsin波、cos波の加算値を使用して学習を行います。 検証ではRNN,LSTMへノイズsin波、ノイズcos波のみを入力し、出力からsincos合成波が 出力されることを確認します。 |
|
実運用を考えた時、ノイズは常に変化し、波形の振幅、位相も、運用時の条件によって変化します。
同一波形を予測するのではなく、ノイズが変化した、振幅を変えた、位相を変えた波形をRNNへ入力し、
0.6周期分の入力波形から2周期〜3周期の波形を予測できるかを検証します。
検証として、学習時と異なるノイズ波形、振幅を変えたノイズsin波、ノイズcos波を RNNへ0.6周期分入力し 2周期〜3周期の波形の平均値、sinCos合成波を予測します。 ランダムノイズ波形を含めて予測することは無意味と思われるので、その平均値を予測します。 RNN個数:20、全波形分割数:100 左図:入力振幅1.0のsinCos合成波 中央:入力振幅0.5のsinCos合成波 右図:入力振幅0.5の理論値sinCos合成波 |
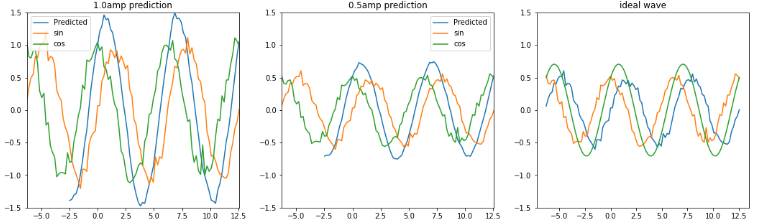
オレンジ色:ノイズsin波
緑色 :ノイズcos波、 青色 :sinCos合成波 入力振幅1.0のsinCos合成波(振幅は±1.4)を予測出来ました、また入力振幅を0.5へ変えましたが、理論値に近い値で予測出来ました。 |
|
学習時と異なる位相、ノイズ波形、振幅を変えたノイズsin波を
RNNへ0.6周期分入力し
2周期〜3周期の波形の平均値、sin波を予測します。
左図:入力振幅1.0のsinCos合成波 中央:入力振幅0.5のsinCos合成波 右図:入力振幅0.5の理論値sinCos合成波 |
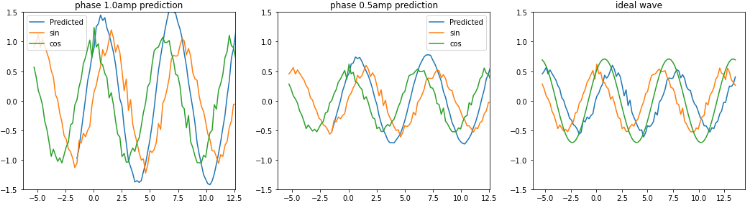
位相と振幅を変えましたが、理論値に近い値で予測出来ました。
|
|
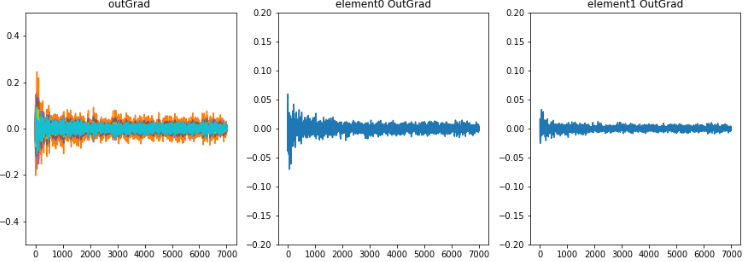
学習時のoutLayerの重みが少し変化したとき誤差の微分値、勾配の推移。
|
 |
|
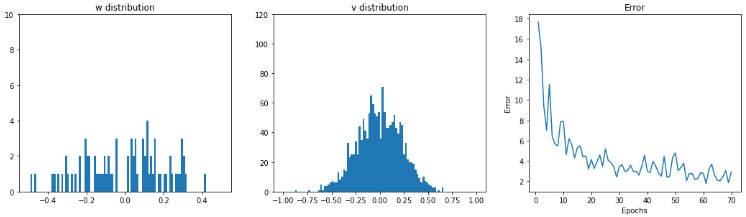
学習時のRnnLayerの重み分布とerrorの推移
 |
|
今回はLSTM(Long short term memory長期短期記憶)を使用します。
前回同様、同一波形を予測するのではなく、ノイズが変化した、振幅を変えた、位相を変えた波形をLSTMへ入力し、
0.6周期分の入力波形から2周期〜3周期の波形を予測できるかを検証します。
学習時間は3倍程度遅くなりますが、予測精度が高くなりました。
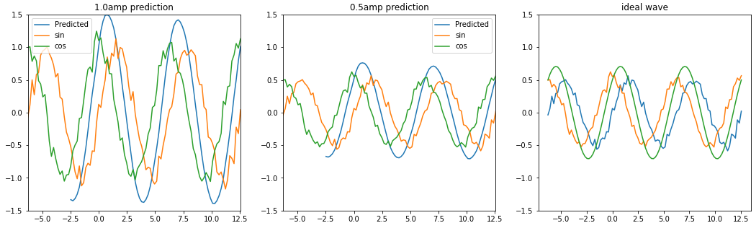
検証として、学習時と異なるノイズ波形、振幅を変えたノイズsin波、ノイズcos波を LSTMへ0.6周期分入力し 2周期〜3周期の波形の平均値、sincos合成波を予測します。 LSTM個数:20、全波形分割数:100 左図:入力振幅1.0のsinCos合成波 中央:入力振幅0.5のsinCos合成波 右図:入力振幅0.5の理論値sinCos合成波 |
 |
|
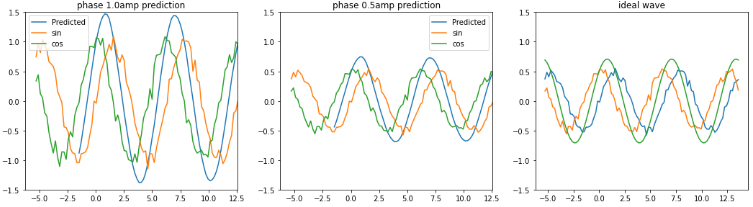
学習時と異なる位相、ノイズ波形、振幅を変えたノイズsin波を
LSTMへ0.6周期分入力し
2周期〜3周期の波形の平均値、sincos合成波を予測します。
左図:入力振幅1.0のsinCos合成波 中央:入力振幅0.5のsinCos合成波 右図:入力振幅0.5の理論値sinCos合成波 |
 |
|
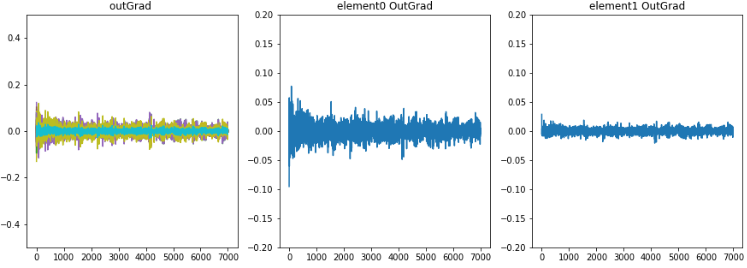
学習時のoutLayerの重みが少し変化したとき誤差の微分値、勾配の推移。
|
 |
|
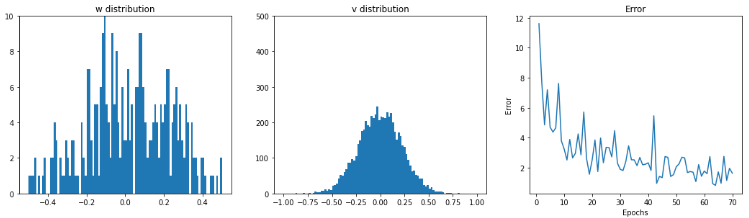
学習時のLSTMLayerの重み分布とerrorの推移
 |