|
デザイン >デジタルFIRフィルタ |
希望とする周波数特性を実現するためには、インパルス応答が下式で与えられ
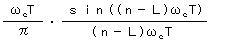
理想的には、次数nが -∞ ~ +∞ で与えられる事が必要です。しかし、実現不可能で次数を有限長とします。
ところが、次数を有限長とすると、ギブス現象と呼ばれるカットオフ周波数付近の近傍にリップルが発生して、
阻止域の減衰量が十分とれません。フーリエ級数の周波数特性を窓関数のように滑らかにした場合、その応答が
速く収束します。よって、希望周波数特性を滑らかなものにします。
インパルス係数に各種窓関数をかけ、周波数特性を滑らかなものにして、振幅特性のリップルを小さくします。
下記に、カットオフ周波数 = 100Hz、サンプル周波数 = 1000Hz、次数 = 20の条件でのインパルス応答と係数を
示します。

理想的には、次数nが -∞ ~ +∞ で与えられる事が必要です。しかし、実現不可能で次数を有限長とします。
ところが、次数を有限長とすると、ギブス現象と呼ばれるカットオフ周波数付近の近傍にリップルが発生して、
阻止域の減衰量が十分とれません。フーリエ級数の周波数特性を窓関数のように滑らかにした場合、その応答が
速く収束します。よって、希望周波数特性を滑らかなものにします。
インパルス係数に各種窓関数をかけ、周波数特性を滑らかなものにして、振幅特性のリップルを小さくします。
下記に、カットオフ周波数 = 100Hz、サンプル周波数 = 1000Hz、次数 = 20の条件でのインパルス応答と係数を
示します。
|
下記は、カットオフ周波数 = 100Hz、サンプル周波数 = 1000Hz、次数 = 20の条件での 窓関数を変えた場合の周波数特性と、その応答のシミュレーションです。 シミュレーションは、理論値では無く、デジタルFIRフィルタのプログラムを作成して、実際に正弦波を入力し、 出力レベルを計測して表示しました。 |
|
下記は、カットオフ周波数 = 100Hz、サンプル周波数 = 1000Hz、窓関数 = ブラックマン固定の条件での 次数を20~50へ変更した場合の周波数特性です。 |
Top項目へのアクセス